Fractals in the Body

Not only are fractals in the world all around us - they are even INSIDE us! In fact, many of our internal organs and structures display fractal properties.


Cast of human lungs, showing blood vessels on one side. Photo courtesy Ewald Weibel, Institute of Anantomy, University of Berne.

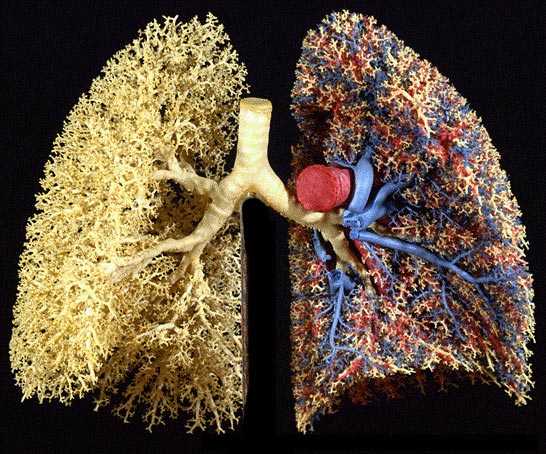
The lungs are an excellent example of a natural fractal organ. If you look at the tree upside-down (mouse over the image), you can see that the lungs share the same branching pattern as the trees. And it is for good reason! Both the trees and lungs have evolved to serve a similar function - respiration. Since they perform a similar function, it should not be surprising that they share a similar structure. This common concept in science is known as the Structure-Function Relationship. Many of the fractals in biological systems we will explore have evolved their structures in order to perform extraordinary functions. In the case of Lungs and Trees, they both breathe. In animals, the lungs breathe in oxygen and breathe out CO₂. In plants, the process happens in reverse. Thus animals and plants are two halves of the same respiratory cycle. But here's the key to their shared structure: They both need a large surface area to function well. The amount of gas (O₂ and CO₂) that can be exchanged through the leaves on a tree or the lungs in an animal is directly proportional to their total surface area. Although the volume of a pair of human lungs is only ~4 - 6 litres, the surface area of the same pair of lungs is between 50 and 100 square meters. That's about the same area as a tennis court!

Note: Remember that natural fractals do not conitnue their branching forever. In human lungs, there are 11 orders of branching, from the trachea to the alveoli at the tips of the branches.

Surface Area : Volume Ratio

In non-fractal shapes, from traditional geometry, there's a simple and important relationship between surface area and volume. Let's examine the surface area to volume ratio for a sphere, a simple, non-fractal shape. The surface area for a sphere, SA = 4πR², and the volume of a sphere, V = 4/3πR³. So the ratio of SA / V is simply 3/R, as the π's and most of the the R's cancel out. This is an inverse function, and it means that when R is large, the SA:V ratio is small, and when R is small, the SA:V ratio is large. We can plot the relationship, and see that it forms a hyperbola.