Fractal Dimension

Simple Dimensions

Before we journey into the strange, new, and fascinating realm of fractal dimensions, let's review a little bit about the standard dimensions we're familiar with. We live in three dimensional space (3D), and for the purposes of this discussion, we'll mostly be ignoring higher dimensions than 3.

A cube, a sphere, and a cone are all simple 3-Dimensional objects.

Circles, squares, triangles and other polygons are 2-Dimensional objects.

Even simpler still is a line, which is 1-Dimensional.

The simplest of all is an infinitely small point, which is Zero-Dimensional.

Of course all of these are mathematical abstractions. A point that really exists cannot be infinitely small. To be 1-dimensional, a line would have to be infinitely thin. And a 2-dimensional plane has no thickness, so a sheet of paper (for example) is only approximately 2-dimensional.

There is another way we can look at simple dimensions, which brings a mathematical significance to the value of the dimension. Examine the patterns in the figure below: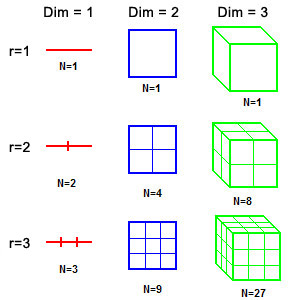

We are going to explore how objects of different dimensions scale as we copy them. Start with a line one unit long, in the upper left of the figure. If we magnify it by a factor of two, we get a line two units long, as shown in the middle left. Magnify it by a factor of 3 and we get a line three units long.

Now do the same with a unit square. If we magnify it by two to form a square with edges twice as long, we end up with four squares. Magnify the unit square by three to have sides that are three units long, and we end up with a square made up of nine unit squares.

Finally, let's do the same thing with a cube of one unit size. Magnify it by a factor of two, so it is two units wide (and long, and tall) and the result is eight unit cubes. Magnify it by a factor of 3 and we get a cube made of twenty-seven unit cubes.

Do you recognize the mathematical pattern in the progressions above? The line expands linearly (1,2,3) as we magnify it, the square expands as the unit squared (U x U or 1,4,9), and the cube expands as the unit cubed (U x U x U or 1,8,27) We can describe the relationship between the total number of objects, N, the magnification factor, r, and the dimension, D, with the following equation:

N = r^D

Hypothetically we could continue the progression to higher, invisible dimensions.

How many unit cubes would exist in a cube that was magnified by a factor r=4, that is, the edge is 4 units long? [ ]

How many unit hypercubes would exist in a hypothetical 4-Dimensional hypercube that is 2 units wide (i.e. r=2)? [ ]

Looking at the equation above, what if we wanted to find the dimension, D, for a shape we didn't know? 'D' is the exponent in the equation, and there's a simple way to solve for it. It just involves using a logarithm, which is the inverse of an exponent. That means we can use a logarithm to cancel out the exponent, we just take the logarithm of both sides of the equation. (Remember, you can do anything you like to an equation, as long as you do it to both sides.)

So if N = r^D, then
log(N) = log(r^D) and one of the cool properties of logs is that
log(r^D) = D*log(r) this means we can solve for D, and:
D = log(N) / log(r)

This means that the Dimension, D equals the log of the number of pieces divided by the log of the magnification factor. Let's try the example of the cube above to see how this equation works. For the cube with the magnification factor r=3, there were 27 little cubes. So D = log(27)/log(3) should equal 3, because a cube is a 3-diemnsional object.

Questions:
Use a calculator to find the value for log(27): [ ]

Find the value for log(3): [ ]

What value do you get for log(27) / log(3)? [ ]

(If you don't have a calculator that does logs, you can use google! Just type in "log(27)" in the search box.)

Next we'll use this idea to explore the dimension of more complex, fractal objects by seeing how they scale with magnification.