Fibonacci FractalsThe Golden RatioThe Fibonacci Sequence appears in many seemingly unrelated areas. In this section we'll see how the Fibonacci Sequence generates the Golden Ratio, a relationship so special it has even been called "the Divine Proportion." Remember that the next number in the Fibonacci Sequence is just made by adding the current number in the sequence to the number before it. Let's see how the numbers in the Fibonacci Sequence compare to each other. In particular, how much bigger is any Fiboncci number than the one before it? If we call the n'th Fibonacci number Fn, then the next number in the sequence Fn+1 = Fn + Fn-1
Let's look now at the ratio of successive Fibonacci Numbers, or 
The ratio of the successive Fibonacci Numbers gets closer and closer to a certain value as n gets larger and larger.
The value it settles down to as n approaches infinity is called by the greek letter Phi or φ, and this number, called the Golden Ratio,
is approximately 1.61803399
The Golden RectangleNow let's look at the Golden Ratio in geometry. The Golden Rectangle is a rectangle whose long side is 1.61803399 times longer than its short side. It has the beautiful property that you can subdivide it by scaling and rotating the same shape to fit inside itself perfectly forever as shown below.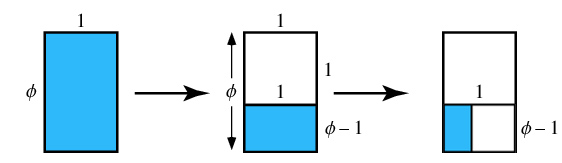
As you can see in the middle panel above, a large Golden Rectangle can be subdivided into a smaller Golden Rectangle, rotated 90 degrees (blue), and a square (white). You can continue this process as long as you like, making a figure full of nothing but golden rectangles and squares at different scales. If you keep filling in the Golden Rectangle by scaling and rotating copies of itself, you can observe a logarithmic spiral emerge: 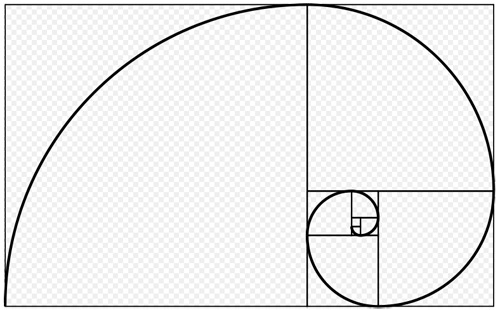 (Will be LevGoldenSpiral Applet!) This type of spiral occurs all over the natural world, even up to the scale of spiral galaxies, It is formed by rotating and expanding a shape at a constant scaling factor. In this case, the scaling factor is the Golden Ratio, so this is called the Golden Spiral. Click "Next" in the applet to cause it to draw a related figure, the Golden Triangle. Here a triangle is rotated and scaled by the Golden Ratio repeatedly. Click "Next" again to see the process repeated witrh a five-pointed star, rotating and scaling by the Golden Ratio at each step. The value of φ can be found all over the five-pointed star. In the figure below, the lengths of the colored segments
are all related to each other through the Golden Ratio. 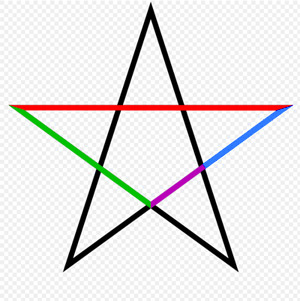
The ratio of the Red to the Green line is the same as the ratio of the Green line to the Blue Line, which is the same as the ratio of the Blue line to the Purple line.
All of these ratios are φ, the Golden Ratio.
It is commonly stated that the Golden Ratio φappears in art, architecture and design, for instance in the proportions of
famous buildings such as the Parthenon in Greece.
It is difficult to really know how common the appearance of φ is, or how it might have appeared in some of the places it is claimed.There
are lots of proportions in nature and art that are close to φ, but the question is, how close? In other words, what is the error
between the ratio of the sides and φ?
|
||||||
|
<- PREVIOUS NEXT -> © Fractal Foundation. |
||||||
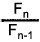 Ratio
Ratio