Fractal Triangle

Learn to draw a fractal Sierpinski triangle and combine yours with others to make a bigger fractal triangle

The Sierpinski triangle activity illustrates the fundamental principles of fractals – how a pattern can repeat again and again at different scales and how this complex shape can be formed by simple repetition. Each students makes his/her own fractal triangle composed of smaller and smaller triangles. Next, students cut out their own triangle and assemble them into a larger fractal pattern that replicates the same shape.

You can use our curriculum for free or can hire us to come to your school to lead fun, hands-on activities. Check out our education and outreach page!

Ages: 1st – 8th grades

Materials:
Markers, crayons or colored pencils
Scissors
Ruler and protractor for older grades
Triangle worksheet

Time:
Approx 30-45 minutes

The template is both on page 6 of the teacher instructions and on page 2 of the student worksheet.

STEAM LESSON PLAN

DOWNLOAD THE INSTRUCTIONS

DOWNLOAD THE WORKSHEET

ANSWER KEY FOR TEACHERS

DOWNLOAD THE TEMPLATE TO DRAW AND COLOR IN– just the blank triangle

DOWNLOAD THE TEMPLATE TO COLOR IN– the Sierpinski triangle drawn out

Teachers – if you have comments or suggestions about this or any of our other fractivities, please email us at 

See what people are saying about this activity on our feedback page!

Orient the template so the triangle points up. Dots show the midpoints of the edges, half way between the corners. Connect the dots as shown below to form a new triangle, pointing down. Color it in.

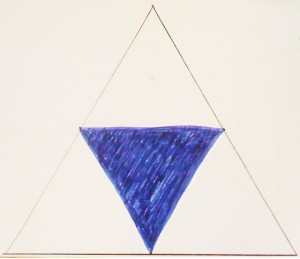
You are left now with three white triangles. Find the midpoints of each of these three triangles, connect them, and color in the resulting downward-pointing triangles.

Each of the three triangles now turns into three smaller triangles, leaving nine small white triangles.

Connect the midpoints of each of the nine white triangles to form 27 smaller downward-pointing triangles. Color those in.

Continue this process for as long as you like, creating triangles in factors of three: 81, 243 or even 729! Use the student worksheet to explore the math behind this and work on mathematical notation.

Be as creative as you wish in coloring the triangles.

When you’re done, cut the big triangle out and write your name on the back.

Next, join your fractal triangle with two other fractal triangles to form a bigger triangle. Then add two more groups of three triangles to form a bigger triangle made of nine triangles. If you’re doing this with your whole class, you can join three groups of nine to make a giant triangle made of 27 individual triangles. If you want to continue, three classes could join all their 81 triangles into an even bigger one. And why stop there???

3rd graders at Apache Elementary School in Albuquerque

If you do this project with your class, please consider contributing your fractal triangles to our Giant Fractal Trianglethon Project to help make the world’s largest Sierpinski Triangle! On April 10, 2011, we built an 8th order fractal triangle, made of 6,561 triangles. Help us reach the next level, and build one out of 19,683 triangles!