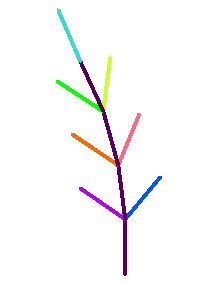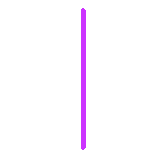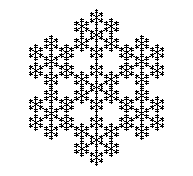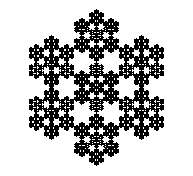Activities Using Fractal Grower
1: Turn Angle and the Penrose Snowflake
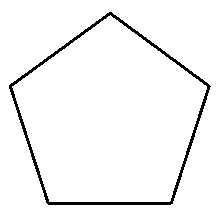
The preset for the Penrose Snowflake has a turn angle of 36 degrees. An image of the axiom of the Penrose Snowflake is shown in figure 1. By changing the turn angle, the axiom has different patterns.
- Find the turn angle that will produce the 5-pointed star shown in figure 2 from the Penrose Snowflake axiom (f--f--f--f--f). As practice for the more advanced activities, first try to find this angle without using the software. Look at figure 2 and try to guess the turn angle. Try using a protractor to measure the angle. Then check yourself with the software.
- What does generation 1 of the L-system you created in part A look like. Again, before using the software, try to draw it out on paper. After trying to draw generation 1 by hand, use Fractal Grower to draw it. Resize the fractal grower window to be about 2 or 3 inches, take a screen capture the drawing, use an image editor to crop the screen capture, and paste it into your solution document.
- Use the sliders and the Next Button, to create a variation of the Penrose Snowflake preset that you think looks cool. Then screen capture, crop and paste this image into your solution document.
- Penrose Tilings, of which the Penrose Snowflake is just one, have a rich history. Research Penrose Tilings on the Internet. Write three original (not copied) sentences about something you find that is interesting about Penrose Tilings.
 |
 |
| Figure 1: Axiom of Penrose Snowflake |
Figure 2: Axiom of Penrose Snowflake
with modified Turn Angle |
2: Turn Angle, Growth, and the Symbols f and !
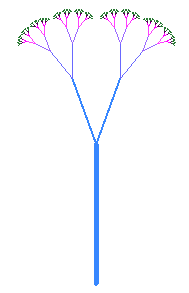
Figure 3 shows generation 7 of the Twig preset. The image is shown on a white
background so that if this document is printed, it will use less ink than it would if the background were black. There are two types of lines in the Twig preset:
Lines drawn by the "f" symbol (These are the tips of the branches) and lines drawn
by the "!" symbol.
The growth slider has no effect on the length of "f" lines, but changes the length of lines drawn by the "!" symbol.
In particular, when growth = 1, "f" lines and all "!" lines have the same length.
When growth is larger than 1, "!" lines get longer with age. New "!" lines are always the same length as "f" lines, but older "!" lines get longer and longer.
What do you think is meant by older "!" lines?
This idea of symbol age is describe in the on-line help, but see if you can figure
out what means by playing with the software.
- By changing the turn angle and growth value it is possible to morph figure 3 into figure 4. Do so, and record the required values of Turn Angle and Growth.
- Starting with the Twig preset, make modifications to the Turn Angle, Growth and Start Angle until you create an image you think is cool. Capture the image and paste it into your solution document. Record the parameters you used to create the image.
 |
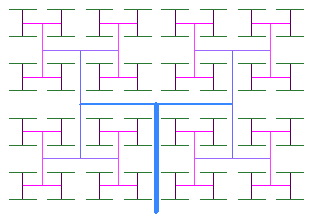 |
Figure 3: Generation 7
of Twig preset
in reverse colors |
Figure 4: Generation 7
of variation of Twig preset
in reverse colors |
3: Changing the Rules
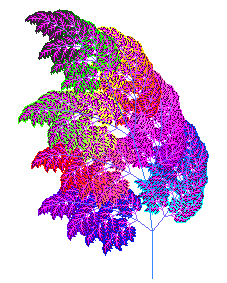
Figures 5 and 6 show generations 1 and 4 of the Fern preset. The axiom for this preset is "f", a single line. The preset has one rule that replaces the "f" with four stem segments (the four "!" symbols in the rule) and with seven branches (three on each side and one at the tip).
- Change the Fern preset rule so that only 4 branches are created. Also change the angle of the branches so that some of the branches are narrower and others are wider. Figure 6 shows an example of generation 7 of the fern preset with only 4 branches and with the relative branch angles changed. You may choose to remove a different three branches. Note: adjustments to the Turn Angle slider change all of the angles and make all larger or all smaller. To make some angles smaller and some larger, you need to change the production rule. Create a fern with 4 branches and a set of branch angles that you find pleasing. Paste a cropped screen capture of generation 1 and a cropped screen capture of a higher generation into your solution document. Record in your solution document the parameters (axiom, rules, turn angle, start angle, and growth) of your creation.
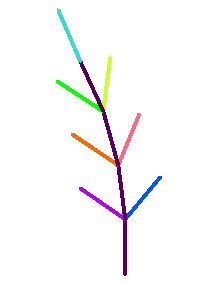 |
 |
 |
Figure 5:
Generation 1 of Fern preset
in reverse colors. |
Figure 5b:
Generation 6 of Fern preset
in reverse colors. |
Figure 6:
Generation 7 of Fern preset
with 3 branches removed and
relative branch angles changed. |
4: Animated GIF
Discover an L-system that looks cool with different values of the growth and turn angle parameters. Create an animated gif with at least 12 frames a morphing of your chosen L-system by varying the growth and/or turn angle. For instructions on how to create an animated gif, see: http://www.htmlgoodies.com/tutorials/web_graphics/article.php/3479881
5: Monogram Axioms
Before attempting to develop the L-system in part 8, it is a good exercise to gain some practice with something simple. Figures 7 shows a monogram of the initials JC that is constructed by generation zero of the axiom af+ffffff+ffffff+ffffff+f+bgffff++gg+ffff+ff. Figure 8 shows a different monogram of the same two letters. The turn angles and start angles are not the same for the two axioms.
The graphical interpretation of an "f" symbol is a straight line.
The graphical interpretation of a "g" symbol is an invisible straight line.
The "+" makes a right or clockwise turn.
The "-" makes a left or counter-clockwise turn.
In both examples, the colors are made by the "a" and "b" symbol and by selecting the option for color by imbedded symbol from the color tab.
- Invent an axiom that will draw a monogram of your initials. Paste your axiom's parameters and a cropped screen capture into your solution document.
 |
 |
Figure 7:
Monogram of initials of lecturer extraordinaire
Joel Castellanos
af+ffffff+ffffff+ffffff+f+bgffff++gg+ffff+ff
|
Figure 8:
Axom: af---fff--f++++ff---bf-ff--ffff--ff-f
|
6: String Substitution: Variables, Terminals and Age
Fractal Grower is an implementation of Lindenmayer Substitution Fractals (L-systems). They are called substitution fractals because they are produced by repeatedly substituting symbols into a string according to some set of rules. For example, the dragon preset has the axiom "f", and the two rules "f=f-h" and "h=f+h". In this L-system, the "f" and "h" symbols are a called variable because with each generation they get replaced with a new string of symbols: Each "f" gets replaced with "f-h" and each "h" gets replaced with "f+h" The symbols "+", and "-" in this L-system are called terminals. A terminal is a symbol in the L-system that does not have a replacement rule. Thus, terminals never get replaced.
The graphical interpretation of both an "f" and an "h" symbol is a straight line.
Figures 9 through 11 show the image and the string of the axiom and the first two generations of the dragon preset. The string of generation 1, has two variables: "f" and "h". The first variable is colored blue and the second variable is colored red. In generation 1, there is only one terminal (the "-" symbol). The terminal in generation 1 is colored black.
In generation 2, the blue "f" is replaced with "f-h". The string "f-h" in generation 2 is colored blue to show that it replaces "f" from generation 1. The terminal "-" from generation 1 goes to generation 2 with no replacement is and shown in black in both generations. Finally, "h" from generation 1 is replaced with "f+h" in generation 2. The string "f+h" is colored red in generation 2 to show that it replaced the red variable in generation 1.
 |
 |
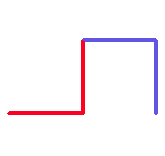 |
Figure 9:
Axom of the Dragon Curve: "f"
|
Figure 10:
Generation 1 of the Dragon Curve.
Axiom "f" was replaced with "f-h"
by the rule: "f=f-h".
|
Figure 11:
Generation 2 of the Dragon Curve.
Gen 1: "f-h" is replaced with
Gen 2: "f-h-f+h".
|
- Figures 12 through 14 show both the image and the string of the axiom and the first two generations of the twig preset. Copy and paste the first and the second generation strings into your solution document. In the string of generation 1, there are two occurrences of a variable (two "f" symbols). The other symbols are terminals. Color the first variable in generation 1 with a blue font and color the second variable with a red font. Leave each of the terminals in generation 1 colored black.
Then, in generation 2, color blue all symbols (veriables and terminals) that replaced the blue "f" in generation 1. Similarly, color red all symbols in generation 2 that replaced the red "f" in generation 1. Finally, leave black all terminal in generation 2 that already existed in generation 1. This is the same thing that was done above with the dragon curve example.
- Because the growth value of the twig preset equals 2.0, the length of lines drawn by "!" symbols doubles each time the "!" symbol ages. In generation 2, some of the "!" symbols are new and therefore, they make lines that are the same length as the lines made by "f" symbols. However, one of the "!" symbols in generation 2 is not new: it was created a generation earlier. This older "!" symbol produces a line twice as long as the new "!" symbols.
In your solution document, copy and paste the second generation strings of the Twig preset. Color red each of the terminals in the generation 2 string that are one generation old. Hint: generation one has 8 terminals, seven of these are new. Therefore, generation 2 will have exactly 7 terminals that are one generation old. The "e" in generation 1 was created in the axiom and will be two generations old in generation 2..
The "f" in the axiom was replaced and no longer exists in generation 1. Variables are always new because they always get replaced.
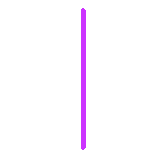 |
 |
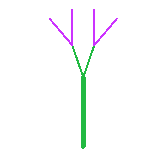 |
Figure 12 Twig:
Axiom
ef
|
Figure 13 Twig:
Generation 1
e![+f][-f] |
Figure 14 Twig:
Generation 2
e![+![+f][-f]][-![+f][-f]]
|
7: Symbol Mapping
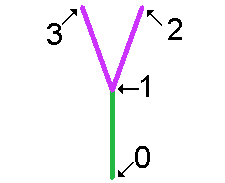
As we have seen, the graphical interpretation of an "f" symbol is to draw a line. The "!" symbols also draw lines, but of length that grows with age. The symbols "+" and "-" create turns. The "e" symbol in the twig preset causes the color of "f" lines to change to lavender. In this section we examine the graphical interpretation of "[" and "]" symbols. The "[" symbol saves the current location and direction of the drawing pen. The "]" symbol restores the previously saved location and direction of the drawing pen.
| Graphical Interpretation of Symbols of Generation 1 of Twig Preset |
| e |
Sets the color of "f" lines to lavender. "!" lines are not affected by "e".
The color of "!" lines is determined by the age of the "!" symbol. |
! |
Draws a line from location 0 to 1. |
[ |
Saves the location and direction at 1. |
+ |
Turns right. |
f |
Draws a lavender line from 1 to 2. |
] |
Jumps back to location and direction at 1. |
[ |
Saves the location and direction at 1. |
- |
Turns left. |
f |
Draws a lavender line from 1 to 3. |
] |
Jumps back to location and direction at 1. |
 |
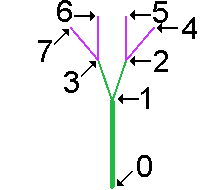 |
Figure 15 Twig:
Generation 1
e![+f][-f] |
Figure 16 Twig:
Generation 2
e![+![+f][-f]][-![+f][-f]]
|
- Create a table like the one above that describes the graphical interpretation of each symbol in generation 2 of the twig preset.
8: Finding a Snowflake
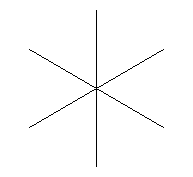
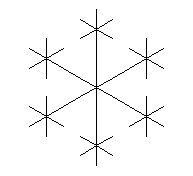
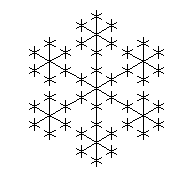
Now you are ready for the hard stuff. Figure 17 shows the axiom an L-system that produces a snowflake pattern. Figures 18 through 21 show successive generations of that system. Your task is to discover the L-system and record it in your solution document.
 |
 |
 |
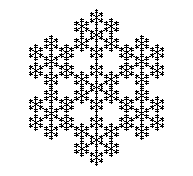 |
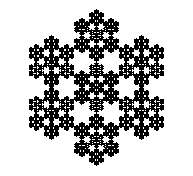 |
Figure 17
Generation 0 |
Figure 18
Generation 1 |
Figure 19
Generation 2 |
Figure 20
Generation 3 |
Figure 21
Generation 4 |
9: L-System Synthesis
Create your own L-system. This should not be a variation of one of the presets, but an original design that is interesting and beautiful. Include in your solution document the axiom, rules and parameters of your system. Also include cropped screen captures either at different generations or with different parameter values.