Fractal Applications

Now that you've gained an appreciation for the fascinating field of fractal math and science, in this final chapter we'll explore just a few of the things that people are already doing with fractals. We'll see examples in the realms of engineering, electronics, chemistry, medicine, even urban planning and public policy. But these illustrations just represent the beginnings of a revolution in how we understand the functioning of the natural world. This is a revolution in which we will apply the lessons learned from the time-tested fractals in nature to inspire more effective and efficient designs for our structures, devices, and systems. And no doubt, the most exciting applications of fractals are still in the future, waiting to be invented.

Cables and Bridges

A modern day recreation of an Inca rope suspension bridge. Image courtesy of Rutahsa Adventures, www.Rutahsa.com.

But first, let's look back a bit, at some fractal ideas people have used for centuries in the engineering of super-strong cables. Long before we built the Golden Gate Bridge, the Inca people in South America were building bridges across mountainous ravines that were hundreds of feet wide. The cables in these bridges were woven by hand out of long strands of stiff qoya grass. Just as in a modern steel cable, a small number of fibers are woven into a larger fiber, several of which are then woven into a larger rope. This repetitive, fractal pattern provides great strength, and it allows a very long cable woven from thousands of individual pieces of grass no longer than a meter or two each.

"Garcilasco de la Vega, in 1604, reported on the cable-making techniques [of the Inca]. The fibers, he wrote, were braided into ropes of the length necessary for the bridge. Three of these ropes were woven together to make a larger rope, and three of them were again braided to make a still larger rope, and so on. The thick cables were pulled across the river with small ropes and attached to stone abutments on each side."^REF

Modern engineers still use this same idea today in the construction of high strength cables that make possible such masterpieces as the giant suspension bridges like the Golden Gate Bridge. A steel cable is formed from a bundle of smaller cables which themselves are formed of smaller bundles, etc.

Golden Gate Bridge, San Francisco. Photo courtesy of Aaron Logan.

Cable technology is essential for building suspension bridges. The Inca weavers and the modern steel cable makers both use a repetitive process to create strong, fractal cable patterns.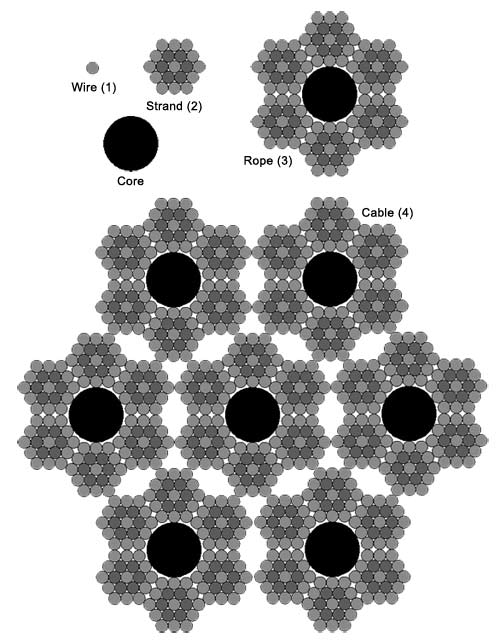

Schematic showing a possible configuration of a steel cable bundle in cross section. Image courtesy of Bernard S. Jansen and Jonathan Wolfe.

The repetitive fractal pattern is evident in this cross-section diagram of the parts of a steel cable, but one thing that's not visible above is that the various 'strands,' 'ropes' and 'cables' are all are wrapped to spiral around each other, which greatly increases the total strength of the cable. The image below shows a piece of steel cable from the side, allowing you to see two levels of self-similar braided structure. Note that the bundles at both scales twist in the same direction.

Image courtesy of Bernard S. Jansen.