From the Simple to the Complex

Complex Numbers

In the last section we iterated the simple equation Z_n+1 = Z_n² + C , starting with the numbers C=1, C=-0.5, and C=-1. We found that the fate of these starting points can be very different: The output of the equation can grow to infinity, it can shrink to a fixed value, or it can alternate stably between two or more fixed values.

Now, we are going to extend our investigation of this iterated equation into 2-Dimensions.To do this, we create a 2-dimensional X-Y plane, and define a coordinate system to describe points in this plane. We call this the Complex Plane, and it consists of Real X-axis and an Imaginary Y-axis.

You can think of Real Numbers as points on the X-axis, Imaginary Numbers as points along the Y-axis, and Complex Numbers as being points in the X-Y plane. The Real axis (X) contains the numbers we're already familiar with. The Imaginary axis (Y) is perpendicular to the Real axis, consisting of what we call imaginary numbers. The basic imaginary number is called i and it is defined as the square root of -1. The numbers are called "imaginary" because no real number can be squared to make -1. Imaginary numbers are multiples of the unit i, such as 3i or -5i.

A Complex Number is a combination of a Real and an Imaginary number. We write a complex number in the form a + bi, where a is the Real component and b is the Imaginary part.

The Complex Plane, showing a point 'C' with a value 1 + 2i.

Although they are not entirely 'real', it turns out that Complex Numbers are very useful in a wide variety of applications, including, physics, engineering, and even art.

The Mandelbrot Set is made from the equation Z_n+1 = Z_n² + C where Z and C are Complex Numbers. In order to be able to compute this equation with Complex Numbers, we must be able to do simple arithmetic like addition and multiplication with them. Fortunately, this turns out to be quite simple, and is illustrated below.

Complex Addition

To add two Complex Numbers, we simply add the Real components with the Real componenets and the Imaginary components with the Imaginary. So for instance, if P = -1 + i and Q = 2 + i, then P + Q = 1 + 2i

We can also look at these points in the Complex Plane as vectors, or arrows pointing from the origin to the point. In this way of looking at Complex Numbers, we can add them by connecting the vectors in a parallelogram.

The new point P+Q can be found by adding the compnents of P and Q, or by connecting the vectors.

Complex Multiplication

It is also possible to multiply two points in the Complex Plane. It is much more convenient to multiply complex points in Polar Coordinates, where we define a point with an angle and a distance from the origin than it is to do the same operation in Cartesian Coordinates, where a point is defined as an (X-Y) pair. To multiply points in Polar Coordinates, we just add the angles of the two vectors, and we multiply their lengths.

Two complex points P and Q can be multiplied to form a new point and vector.

When we calculate the Mandelbrot Set equation, we need to square the complex number Z. To do this, we're simply multiplying Z x Z, which by the rule given above just means doubling the angle and squaring the length of vector.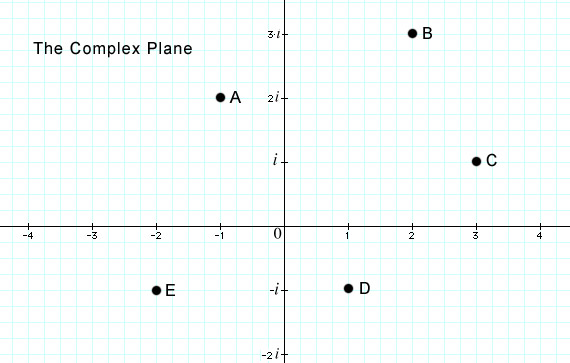

Questions:
The graph below shows several points in the complex plane. Please determine the coordinates for each point in the form a + bi. For example, point A = -1+2i.

Now that you have seen the concept of iterating an equation, and understand the 2-Dimensional coordinate system we'll use, we can move into the next section. We'll see what happens when we iterate the equation Z_n+1 = Z_n² + C and look at the fates of various starting values of the complex point C.