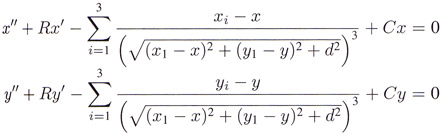Strange Attractors

Now let's turn our attention to another chaotic system that is perhaps a little easier to grasp. This time we'll examine the behavior of a simple mechanical device that generates extremely complex patterns.

The Magnetic Pendulum

Consider a pendulum with a magnet at the end of it, as shown above. The pendulum swings freely between three magnets, colored blue, red and yellow. The magnetic pendulum is equally attracted to each of the three magnets, and it will eventually come to rest over one of them. But the ending point depends very sensitively upon the starting point. As you might expect, if you start the pendulum over one of the magnets, it will remain over that magnet. But if you pull the pendulum somewhere else and release it, the fate of the pendulum is very difficult to predict.

Three traces are shown below, where the pendulum is started from very similar starting positions between the blue and yellow magnets. However, the pendulum follows completely different trajectories in each case, and it comes to rest on different magnets.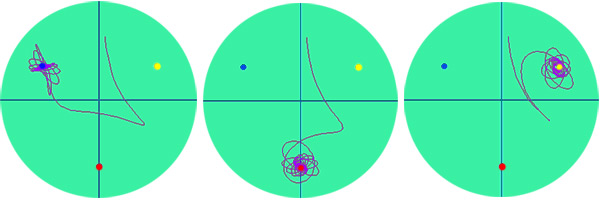

Reproduced with permission from Drexel University, copyright 1997 by
The Math Forum @ Drexel. All rights reserved.

Let's see if we can describe the strange attractor for this system, that is, a map of the outcomes for all the possible starting conditions of the pendulum. For every starting point, a computer simulation will determine the final resting point of the pendulum, and we'll color the starting point the same color as the magnet where the pendulum stops.

Image courtesy of Paul Nylander.

This attractor is extremely complex. Every starting point in a yellow area means that the pendulum will come to rest over the yellow magnet, and so on. Because the setup is symmetrical, the attractor is also symmetrical. Notice the fine detailed structure in the attractor throughout much of the image, which reflects the sensitivity to initial conditions, i.e. that small changes in the starting position can result in big differences in the outcome.

Question:
Are there any starting points in the image above where the pendulum WON'T end up over one of the three magnets? If so, where? [ _____ ]

Alas, the equations that simulate the motion of a pendulum in 3D under the influence of three magnets are much too complex to calculate the behavior in real time. In fact it takes several hours to compute an attractor like the one above. If you want to explore the behavior of this pendulum in real-time, you'll have to build one!

The differential equations are shown below, so you can see the math that models the behavior of the pendulum's motion and that creates this strange and beautiful attractor.

Equation reproduced from "Chaos and Fractals", Peitgen, Jurgens, Saupe.