Fractal Geography

Fractal Rivers

As we saw in the first chapter, rivers are a great example of a natural branching pattern. They are formed by repeated erosion following thousands or millions of years of rain falling and draining away downhill.

Small streams (called 'tributaries') merge together to form bigger rivers, which join with other rivers, and eventually they empty into a lake or the ocean. The fractal geography of rivers explains a basic mystery of rivers:

The answer is that the network of tributaries collects water from a huge surface area of land and funnels it into the river. Even though it may not have rained recently where you happen to be watching the river, somewhere upstream it probably rained on some of the tributaries, possibly hundreds or sometimes even thousands of kilometers away.

Figure 1. Tributaries joining the Rio Grande at Elephant Butte reservoir. Image courtesy of Google Earth.

A watershed, also known as a drainage basin, is an area of land where any rain that falls will drain into the same river or body of water. Watersheds are very important to understand, as they illustrate the functional interconnectedness of land.

Watersheds - Basins of Attraction A watershed is also a real-world example of the mathematical concept of a Basin of Attraction. We learned about the Julia Sets in Chapter 5 which can be seen as basins of attraction for starting points in complex space. Any point in the black are of a Julia Set will be attracted to a fixed finite point inside the basin of attraction. To draw the analogy further, any rain falling inside the black area would drain (be attracted) into a lake at the center, while any rain falling outside the basin would be attracted elsewhere. In the case of a Julia Set, the points outside are attracted to infinity, while in a watershed, rain falling outside is 'attracted' (or drains) into another river or lake.

Figure 2. A diagram of all the tributaries that make up a river drainage basin. Figure 3. A closed Julia Set, where any starting point in the black area is attracted to a fixed point inside the basin.

Watersheds can be tricky to interpret on a map, and - like any good fractal - they exist at multiple scales. The map above shows the main watersheds of the state of New Mexico. Rain that falls in the central part of the state drains into the Rio Grande river. The Rio Grande basin (labeled '13') is divided into two parts: the left drains directly into the Rio Grande, while the basin on the right drains into the Pecos River. They are grouped together because the Pecos River joins the Rio Grande further south in Texas, before the Rio Grande empties into the Gulf of Mexico and the Atlantic Ocean.

On the west side of the state, there are two separate basins, '14' and '15', which drain into the Upper and Lower Colorado River. These two rivers join further west, at Yuma Arizona, before emptying into the Sea of Cortez and the Pacific Ocean.

The line dividing the Rio Grande basin from the Colorado River basins is extremely important. It is part of the Continental Divide. Rain that falls to the west of this line will drain into the Pacific Ocean, while rain that falls on the east of this line (even if it's only a few meters away) will end up following a radically different path and draining into the Atlantic Ocean. This is a great illustration of the chaos theory principle of Sensitivity to Initial Conditions, in which small differences in the starting conditions lead to big differences in the outcome.

Let's look at the watersheds of New Mexico a little more closely. The map in Figure 4, above, of New Mexico's watersheds shows 6 main watersheds, each in a different color. Each of these watersheds is further subdivided into several smaller basins. It's important to realize that the squiggly black lines are NOT rivers, but they are the boundaries of the sub-basins within each watershed.

Question:
How many line sub-basins can you count in the Lower Colorado Watershed, labeled '15' in Figure 4? [ ]

We can zoom in a little and look closer at the section for the Rio Grande Basin. Compare the figure below with the one above, to see how they relate to each other.

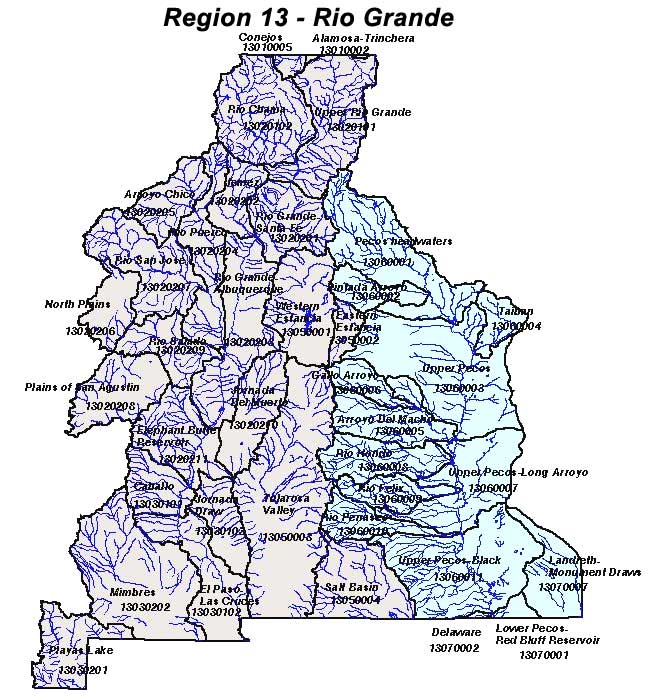Figure 5. Map of the watersheds of the Rio Grande Basin. Image courtesy of NM Water Resources Research Institute.

At this scale, we can see some of the small tributaries that collect rain from within each of the sub-basins. This map takes a little while to figure out. The Rio Grande itself is difficult to pick out, since all the rivers are colored alike, regardless of their size. You can find the Rio Grande at the south edge of the map where it crosses into Texas, just below Las Cruces.

Of course, watersheds are fractal in nature, so we could keep zooming in and looking at smaller and smaller watersheds, that is sub-basins of the sub-basins. Even at the very local level of arroyos (small, often dry creeks) on the side of a hill, you can define small scale versions of watersheds, distinguishing the branches of the network of arroyos that are directly connected from those that are more distantly connected.

Watershed Engineering Why do we care about watersheds? Water is critical to all life, and our entire civilization is dependent on the distribution of water. Water distribution is what watersheds are all about. Sometimes two rivers may be relatively close together, and yet in totally different watersheds, on opposite sides of a divide. In this case, it may sometimes be practical to divert water from one watershed to another. This is currently being done in the ambitious San Juan - Chama diversion project, in which water from tributaries of the San Juan River (in the Colorado River watershed) is being diverted through tunnels into the Chama River (part of the Rio Grande watershed). Four tunnels and a canal, ranging from 5 to almost 13 miles have been built to carry 110,000 acre-feet of water per year into New Mexico. Rather than pump the water up and over the continental divide, tunnels through the mountains provide a connection from one watershed to another. REF One acre-foot is the volume occupied by water covering an acre, 1 foot deep, and is equal to 325851 gallons.

Map showing the location of the San Juan - Chama diversion tunnels. Image courtesy of ABCWUA.

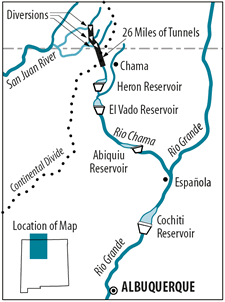
Question:
How many gallons of water are diverted through the San Juan - Chama project each year? [ ]

How many gallons is that each day? [ ]