Branching Fractals

Perhaps the most remarkable thing about the study of fractals is that there are fractal patterns all around us! Even if you don't think you know anything at all about fractals yet, you actually already do, because you've grown up in a world full of fractals. In this first chapter we will first learn about natural Branching fractals, and then about Spiral fractals.

A fractal is a pattern that repeats at different scales, and examples are all around us. Technically, we call shapes like this "Self-Similar" because a little piece of the shape looks similar to itself. This fern shows a rough self-similarity, being made of little copies of the same overall shape.

A fern is an ancient, primitive plant that is made up of the same pattern at different scales. Photo courtesy of Jonathan Wolfe.

Fractal Trees

The plant kingdom is full of fractal patterns, and while we have only started calling these patterns 'fractal' since the 1970's, people have been observing these kinds of patterns for much longer. Perhaps the first description of a fractal pattern in nature came from the great artist and scientist Leonardo da Vinci in the 15th century.

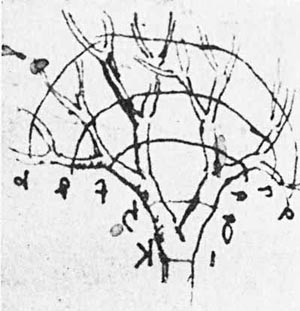
Leonardo da Vinci speculated about a logical relationship between tree branches at different heights, based on their volumes. One branch, the trunk, splits in two, which he thought must have 1/2 the cross-sectional area as the trunk. These two branches then split into four, whose area would be one fourth that of the trunk.

Leonardo wrote in his notebooks: "All the branches of a tree at every stage of its height when put together are equal in thickness to the trunk [below them]." This was a logical inference, and has come to be known as Leonardo's Rule for Branches. This came from the idea that branches act as pipes to move fluid, and the total cross-sectional area must be the same at different levels of the tree. This rule has actually been shown to be not entirely correct (Ref), but it is a good initial model.

Elm trees. Photo courtesy of Jonathan Wolfe.

There are a few things to notice about the fractal structure of a tree. First of all, a tree is approximately self-similar. That is, a small piece of the tree looks somewhat like an entire tree. Secondly, while a tree is a large, complex object, it is formed by repeating a simple process over and over again. This is a basic principle that we will see over and over again in all the various fractals we'll encounter, whether in nature, on paper, or in a computer.

The essential, basic process by which a tree grows is this:

A sprout comes out of the ground, and then splits into branches. Each of these branches then splits again into new branches, and each of these branches splits again into new branches. At each point in this process, it is as if two new, smaller trees emerge, and the new branches can be thought of as the trunks of the next generation of trees. So a large tree can be seen as a collection of many smaller trees of various sizes. Thus the repetition of branching that forms the tree also generates the tree's self-similarity. In plant science, the branching points are called 'nodes', and the branches themselves 'internodes'. In general mathematical terms, we refer to the branching points as "bifurcations" and the internodes as... "branches." We will see many examples of bifurcations in our exploration of fractals.

Note: Natural fractals such as trees and ferns do NOT keep repeating their patterns forever. The mathematical fractals we will encounter in a few weeks, such as the Mandelbrot Set, DO go on forever. At some point, the fractal repetition breaks down in natural patterns, and they cease to be fractals.

We can find fractal patterns over a wide range of scales in nature, and we can see a similar branching pattern in the veins of a tree's leaves. We will soon see examples of natural fractal patterns that are much larger - and smaller - than these.


Questions:
Refer to Leonardo's sketch of a tree above. Let's call the tree trunk the zero order branch. When it splits in two, we'll call these the first order branching, and there are two of them. When these two branch again, it is called the third order branching, and there are four of these 3rd order branches.

What is the highest order of branching that Leonardo shows in his drawing? [ ]
How many of the highest order branches are there [ ]
If a tree followed this same progression, and had 8 orders of branching, how many 8th order branches would it have? [ ]
If this hypothetical tree had 8 orders of branching, how many branches total would there be (8'th order + 7th order + 6th order, etc)? [ ]

Fractivity:
Go outside and find a tree to study. Smaller and simpler trees are better for this exercise. Count how many orders of branching the tree shows. It's very difficult to count all the higher-order branches on a tree, so we'll focus on the first few orders.
Fill out the tables below:
Tree 1
How many zero order branches are there? [ ]
How many first order branches are there? [ ]
How many second order branches are there? [ ]
How many third order branches are there? [ ]

Now, find a different tree of the SAME species, and repeat your data collection for this tree:
Tree 2
How many zero order branches are there? [ ]
How many first order branches are there? [ ]
How many second order branches are there? [ ]
How many third order branches are there? [ ]

Finally, find a tree of a DIFFERENT species, and repeat your data collection for this tree:
Tree 3
How many zero order branches are there? [ ]
How many first order branches are there? [ ]
How many second order branches are there? [ ]
How many third order branches are there? [ ]

Do your results match the idealized drawing of Leonardo's tree? [ ]
Do the two trees of the same species have the same number of branches of each order? [ ]
Do the trees of different species have the same number of branches of each order? [ ]