 We saw in the previous section that nature is full of fractal patterns. Many of these structures take on branching or spiraling patterns,
and we saw how simple processes, repeated over and over again, could create these complex patterns. In this chapter, we will explore these same sorts
of repetitive process, but this time in the realm of pure geometry. We will learn about the power of iteration to create complex fractal patterns,
through the exploration of Iterated Function Systems, and we will see some of their extraordinary properties. We will even learn the special language of L-Systems
that describes how we can iterate simple systems to create realistic plant-like structures.
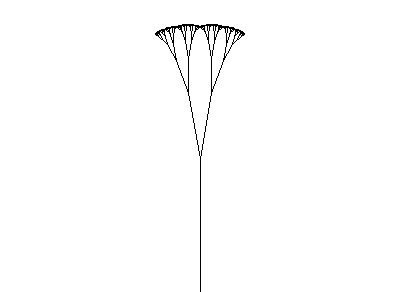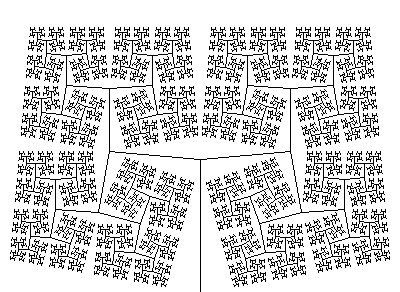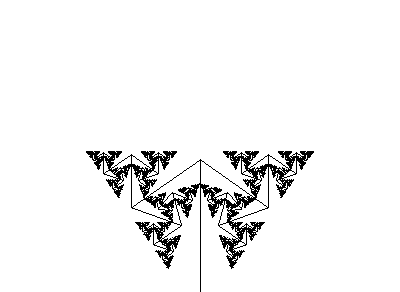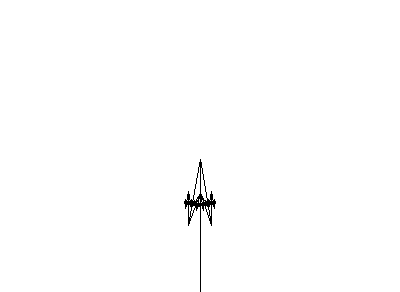
Sierpinski FractalsThere are many ways to generate geometric fractals. First we will begin with the process of repeated removal, and an exploration of the Sierpinski Triangle. Starting with a simple triangle, the first step, shown in the figure, is to remove the middle triangle.
This leaves behind 3 black triangles surrounding a central white triangle (iteration 1).
We can then repeat the same process, at a smaller scale, and remove the middle third of each of the three triangles, giving us the second iteration. At this level, we have 9 smaller black triangles remaining.
The number of smallest triangles triples again in the third iteration, to 27. Level 4 has (27 * 3) = (9 * 9) = 81 tiny triangles.
 Questions: How many smallest black triangles will there be at the 5th iteration? [ ] How many smallest black triangles will there be at the 8th iteration? [ ] Another fractal we can make using the process of repeated removal is the Sierpinski Carpet. To create this shape, we start with a square, divide it in 9 smaller squares and remove the central square. Then repeat the process with each of the remaining 8 squares.  5th order Sierpinski Carpet There is one 1'st order white square and nine 2'nd order white squares in the figure above. How many of the smallest white squares will there be at the 5th iteration? [ ] How many 6th order squares would there be if we continued the process? [ ] There are two ways to solve these problems. The first way is to discover and use a formula that tells you how many squares are created at a given iteration. The second method is simply to count all the squares at a given size. If it took you 1 second to count each square, regardless of its size, how long (in minutes) would it take you to count all the white squares in the image above? [ ] How long (in minutes) would it take you to count all the squares in a 6th order Sierpinski Carpet? [ ] |
|
<- PREVIOUS NEXT -> © Fractal Foundation. |