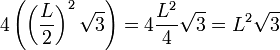Sierpinski Fractals - in 3D

Now let us continue exploring these fractals in 3 Dimensions. (Although we'll learn in Chapter 9 on Fractal Dimensions, that these objects are not quite fully 3-Dimensional!)


The Sierpinski Tetrahedron (sometimes called the Tetrix) is created by starting with a tetrahedron and removing the middle tetrahedron, and then repeating this process, just as we removed the middle triangles to form the Sierpinski Triangle.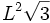

Click and drag the Sierpinski Tetrahedron above to rotate it. Play with it to get a feel for it from different angles.
Next, <Ctrl>-click the shape to lower the number of iterations, eventually reaching a simple tetrahedron, the 0'th order. <Alt>-click the shape to raise the number of iterations. The 1'st order shape is made of 4 tetrahedrons. Play with this shape, and then <Alt>-click to generate the 2'nd order shape. (Be careful not to go too high or you will crash your browser!)

Questions:
How many of the 2'nd order tetrahedrons are there? [ ]
<Alt>-click the shape a few more times to raise the number of iterations. Create a formula to tell you how many tetrahedrons exist of a given order.
How many of the 6'th order tetrahedrons are there? [ ]


Now let's explore the surface area and volume of the Sierpinski Tetrahedron.
The formula for the surface area of a plain tetrahedron is:


where L is the length of one edge.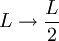

How do we calculate the surface area of the first order Sierpinski Tetrahedron? Well, it's made up of 4 copies of the original tetrahedron, where the length of each edge is only half of the original length,



So if we substitute L/2 in the formula for the area, we can find the area of one of the smaller tetrahedrons. But, there are four of these tetrahedrons, so we have to multiply the area by 4.


This tells us that the area of the 1'st order Sierpinski Tetrahedron is the SAME as the area of the 0'th order Tetrahedron. We can continue this process, and discover that the surface area decreases by a factor of 4 each iteration, and the number of tetrahedrons increases by a factor of 4. This means that the surface area stays the same at each iteration.

The total volume, of the Sierpinski Tetrahedron however, decreases by a factor of 2 at each step. At the logical limit of infinite iterations, the volume decreases to zero, but the surface area remains constant.
This is a very strange property!

Questions:
If the surface area of a 2'nd order Sierpinski Tetrahedron is 100 cm2, what is the surface area of the 4th order shape? [ ]

If the Volume of a 0'th order Sierpinski Tetrahedron is 256 cm3, what is the Volume of the 5th order shape? [ ]

Now let's translate the square Sierpinski Carpet into the cubic fractal know as the Menger Sponge. Another name for this could be the Sierpinski Cube.




Again, we can click and drag the object above to rotate it. Play with it to get a feel for it from different angles.
Next, <Ctrl>-click the shape a couple of times to lower the number of iterations, reaching a simple cube, the 0'th order. <Alt>-click the shape to raise the number of iterations. (Again, don't go too high or your computer will struggle to render the image!)

Interestingly, it can be shown that the Surface Area of the Menger Sponge increases with each iteration, while the Volume decreases with each iteration. Thus, at the logical limit of infinite iterations, the Volume goes to 0, and the Surface Area goes to infinity (∞). Again, this is a very strange property!

The 1'st order shape is made of 20 smaller cubes, and the 2'nd order shape is made up of 400 tiny cubes.

Question:
How many of the smallest scale cubes are in the 3'd order Menger Sponge? [ ]




Play with the cubic fractal above. <Ctrl>-click the shape a couple of times to get to the 0'th order cube. Figure out the process of removal that generates this fractal.

Questions:
How many cubes are in the 1'st order shape? [ ]

How many cubes are in the 2'nd order shape? [ ]

How many cubes are in the 3'nd order shape? [ ]


<- PREVIOUS      NEXT ->


© Fractal Foundation.