Mandelbrot Magic

Universality

It is one of the most amazing discoveries in the realm of mathematics that not only does the simple equation Z_n+1 = Z_n² + C create the infinitely complex Mandelbrot Set, but we can also find the same iconic shape in the patterns created by many other equations. In fact, the phenomenon of Mandelbrot Universality means that anytime we iterate a function that in some portion, at some scale, resembles the parabolic function Z², then we will find small copies of the Mandelbrot Set in the map of that function.

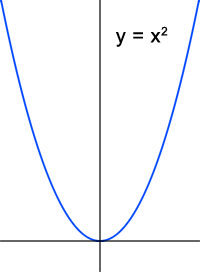
Let's see what this looks like. When we plot the basic function that generates the Mandelbrot set, Z², we find the parabola, shown below, at the left. Now let's look at a different function, the sine wave, which is plotted below on the right. These two functions are very different, and yet they share enough of their shape in common that iterating the sine function in the complex plane and mapping the fates of the starting values creates a fractal image... that contains small replicas of the Mandelbrot Set!^REF

Let's see some examples! Below you can see the fractal generated by iterating the equation:

On the left is the big view of the fractal image, and on the right is a zoomed in detail, showing one of the infinite number of Mandelbrot replicas in this fractal.

Fractal generated with a sinusoidal function, showing a Mandelbrot Set replica.

Let's look at another example. This next fractal has been called the 'Nova' fractal, and it is generated by iterating the equation:

On the left is the big view of the Nova fractal, and on the right is a zoomed-in detail, showing a perfect Mandelbrot replica.

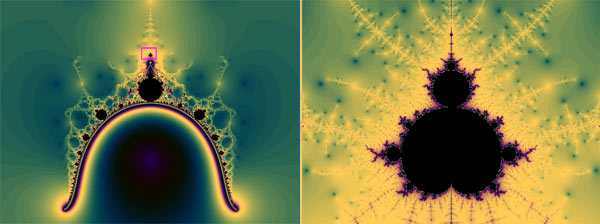The Nova fractal, discovered by fractal explorer Paul Derbyshire.

Finally, let's examine the "Magnet" fractal, which is particularly interesting, because it comes from an equation in physics that describes the way in which metals such as iron can gain or lose their magnetism. The equation is: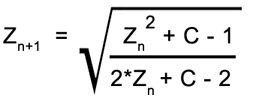

"Magnet" Fractal generated with a function describing the phenomenon known as magnetic percolation.

As if the Mandelbrot Set itself were not an infinite enough playground to explore, we now have thousands of other formulas to play with that generate a dazzling variety of fractal forms!